Aquesta setmana he fet una activitat que m’ha funcionat molt bé. Reconec que em movien més les ganes de provar la meva nova joguina que l’activitat en sí. Per això m’ha sorprès l’èxit, ara, després de fer-la i de pensar-hi una mica, m’adono que és una activitat petita i potent. M’ha resultat molt útil per iniciar la classe, per entrar en clímax de treball, per fer oblidar la bogeria del patí.

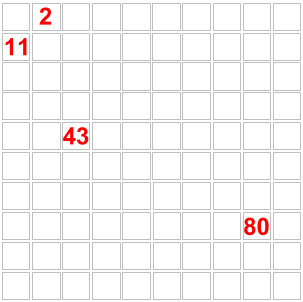
Consisteix en un senzill exercici numèric combinat amb una dinàmica de participació que el fa més atractiu. L’activitat parteix del panell del pictograma. Presento la graella de la centena, els explico que, entre d’altres coses, serveix per contenir els nombres de l’1 al 100. Mostro que hi ha uns nombres ja col·locats (de color vermell), insisteixo en que estan col·locats al seu lloc, i els dic que tenen prou informació per col·locar la resta de números.

Arribats aquí explico la dinàmica (que he tret d’aquí):

• Qui vulgui participar ha d’alçar el braç.
• Qui surt pot triar entre dues opcions: (1) agafar un número a l’atzar i col·locar-lo allà on cregui que va, o bé (2) modificar un (i només un) nombre dels que hi ha la graella si creu que està malament.
• Durant tot l’exercici no es pot comentar res en veu alta.

És tan difícil com clau mantenir el silenci mentre van sortint, sobretot si hi ha nombres fora de lloc. Tots/es volen dir la seva quan detecten un error, i fer notar que estaven al cas quan es rectifica una errada. És necessari fer-los veure la importància de respectar el silenci, d’aquesta manera tothom pot tenir una relació personal amb la graella i no es pertorba el pensament dels demés. Alhora, és el que manté la tensió de l’activitat, tothom pot trobar el seu moment per entrar.

Hi ha un punt en què s’adonen que la graella té 121 caselles, i no 100, com la majoria han pressuposat, descobreixen llavors que no totes les caselles han d’estar plenes. Arribat aquest punt comencen a no fer errades i seguir col·locant nombres no aporta gaire, és el moment de parar. Ells/es tenen ganes de seguir, tots/es han descobert algun patró, han creat les seves regles i ho volen seguir demostrant, cada nombre és un petit èxit.

L’activitat no ha acabat, els dic. És el moment de posar en comú els descobriments que han fet. Què heu descobert? Per què al principi fallàvem i ara ja no? Quines regles, quins patrons heu trobat? Què us has fet adonar? Qui vol explicar algun descobriment? Sorpresa: quasi tots els braços alçats. Normalment em costa aconseguir que exterioritzin els seus pensaments.

Resulta impossible reproduir les converses que s’han donat, als quatre grups (1r d’ESO) han estat riques i similars, però cada conversa ha tingut personalitat pròpia. Alguns dels seus descobriments:

• La graella té 11 nombres a cada costat, si hi van els nombres de l’1 al 100, en sobra un “per cada banda”. Tots descobreixen això gràcies al silenci i la relació personal amb la graella.
• Els nombres de la columna 5 acaben en 5. Els nombres de la columna 2 acaben en 2. … I pregunto, se us acudeix com generalitzar aquesta regla per totes les columnes? Sí, se’ls acudeix.
• Se us acudeix una regla similar per les files? Costa més, però sí, se’ls acudeix. Els nombres de la fila 3 comencen per 2. Podem generalitzar-la?

Estic segur que se’n poden treure moltes coses més.

En general s’expliquen malament, fan servir paraules errònies (no diferencien entre files i columnes), s’expressen amb imprecisió (abusen dels adverbis això, allò…), etc. Ara m’adono que les normes per vetllar per un bon ambient d’aula m’han servit a mi per canviar la manera d’afrontar aquestes converses. Abans estava en “busca i captura” de la resposta perfecta, quasi totes les respostes dels alumnes les trobava incompletes (de fet, ho són), i creia que ajudava els alumnes afegint el que hi trobava a faltar. Ara, mentre expliquen les seves descobertes els faig més preguntes per ajudar-los a matissar les seves paraules, intento estirar de les seves paraules sense rectificar res del que diuen, al contrari, miro de rescatar el que sigui. Darrera de cada resposta hi ha idees potents, ningú no diu res que no cregui que valgui la pena sé dit. Alhora, en aquestes edats, el decalaix entre el que es diu i el que es pensa és brutal, és clau ajudar-los a reduir aquesta distància (dec aquest idea a la meva companya Maria Beneyto).

Nota: No cal disposar del tauler per fer l’activitat, poder tocar els nombres i interaccionar-hi físicament té un valor especial que no sé explicar, tot i així hi ha bones alternatives digitals.