Després del primer contacte amb l’ús de símbols per representar quantitats, traduïm expressions literals a llenguatge matemàtic.
El doble d’una quantitat (2·n), o la meitat (n/2).
El següent nombre d’un nombre donat (n+1).
Un nombre multiplicat per quatre més tres (4·n+3).
Tres més un nombre tot multiplicat per dos ((3+n)·2).
La suma de tres nombres consecutius (n+1+n+2+n+3).
Un nombre multiplicat per si mateix (n·n, o n² si escau).
…
I segueixo amb aquesta petita activitat sense paraules per introduir el valor numèric:
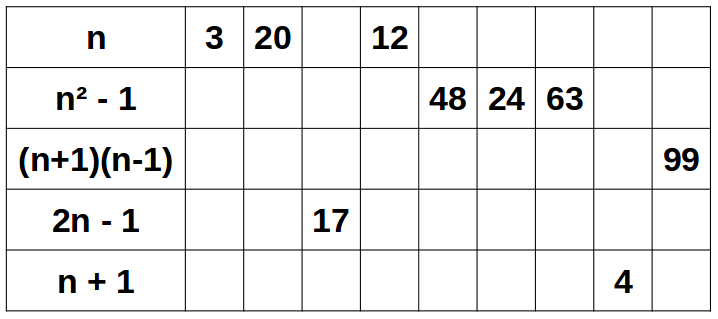
Veieu aquesta taula?
Podeu fer dues coses, (1) sortir i col·locar un número nou o (2) si creieu que hi ha algun que estigui malament, sortir i corregir-lo. Us asseguro que els que hi són tots correctes.
Hi ha una regla d’or: silenci sepulcral. Fins i tot quan detecteu un error, l’única manera de corregir-lo és demanar torn i sortir a la pissarra.
Qui sàpiga col·locar un número que aixequi el braç. Algú vol començar?
Si ningú aixeca el braç, poso jo el primer número. Als meus alumnes els ha encantat aquesta activitat. I a mi també, es crea una dinàmica de participació molt maca.

10 comentaris
He fet aquesta activitat a classe i la veritat ens ha encantat a tots. Han participat i han seguit les indicacions perfectament. El que més m’ha agradat a mi ha estat com han anat agafant confiança. Em preguntaven ‘i si m’equivoco què passa ?’ i els hi deia ‘res, algú altre ja ho canviarà’ i ha fet que perdessin la por a equivocar-se (que en tenen molta).
Hola,
Les meves sensacions en fer-la coincideixen amb les teves. La dinàmica convida a participar, no penalitza en excés les errades, però alhora convida a pensar i buscar la resposta correcta. Per altra banda, aquest tipus de situacions es poden aplicar a moltes altres situacions d’aula.
Gràcies pel teu comentari,
Sergi
Sí, també l’he fet jo i els ha encantat. La dinàmica de participació molt maca. En acabar demanaven tornar a jugar-hi! Amb la mateix o una altra taula. Gràcies per compartir.
Hola Sergi!
Hem emprat la teva proposta a l’aula de 2n d’ESO i ha estat un èxit!!! Fins i tot que no hi hagués silenci sepulcral ho he trobat genial, ja que s’han engrescat molt i no es podien contenir, es solapaven resultats i es “picaven” entre ells. Han participat tots els alumnes.
Gràcies!
La meva proposta no és meva, és teva.
Felicitats.
Sergi
Aquesta activitat de la taula amb post-it’s m’ha agradat, la faré servir. Gràcies. I també amb la prèvia de l’expressió algèbrica dels literals…
Tanmateix la suma de tres consecutius no és pas (n+1)+(n+2)+(n+3), no si el nombre ha de ser n. Això els confondria; cal dir n+n+1+n+2, és a dir 3n+3
Què bé que t’agradi Ramon.
(n+1)+(n+2)+(n+3) són tres nombres consecutius.