Quants quadrats hi ha al perímetre d’aquesta figura?
I si enlloc de tenir 6 quadrats de costat en tingués 7?
I si en tingués 8?
I si en tingués 43?

Arribats fins aquí s’indueix la necessitat d’usar un mètode, de generalitzar l’estratègia. Així doncs…

I si el costat tingués un nombre qualsevol de quadrats, posem per cas n quadrats, podríem expressar el nombre de quadrats del perímetre en funció de n?

Sí, poden i surten diverses expressions algebraiques fruit de les diferents estratègies d’aprenentatge de cadascú.

Si totes les expressions són correctes (es poden comprovar amb els casos anteriors), com és possible que surtin diferents expressions?

Les escrivim totes a la pissarra i surt un representant de cada expressió algebraica a explicar què ha pensat per arribar a aquesta solució.

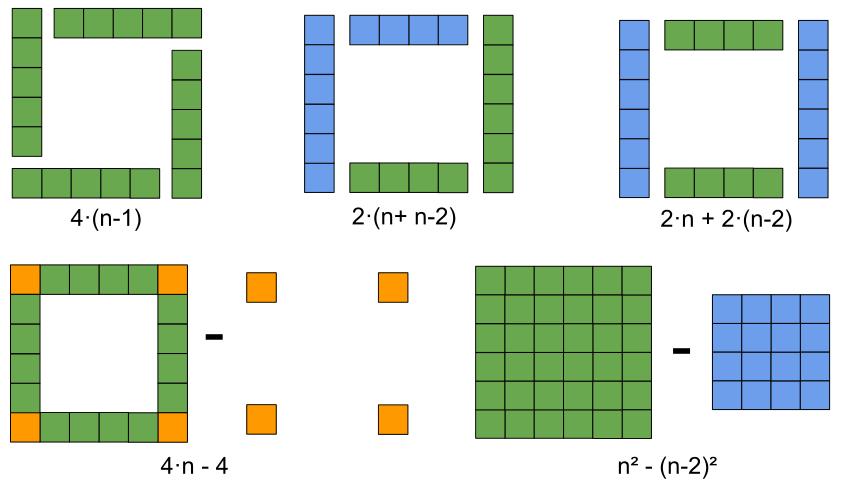Revisem conjuntament les explicacions dels representants, i també podem assegurar-nos de que totes són correctes donat comprovant els casos n=6, 7, 8 i 43 de l’inici.

I doncs, si totes les expressions algebraiques són correctes, per què són diferents?

Sabem que són iguals però no per què, es crea la necessitat de trobar un lligam entre les diferents expressions, de manipular-les algebraicament.

Arribats fins aquí, fixem la manipulació d’expressions algebraiques?

Crèdits: A partir d'una idea (més completa) de l'Abraham de la Fuente.