Després de motivar l’estudi de l’àlgebra, introduir l’ús del llenguatge matemàtic per parlar de quantitats desconegudes, i crear la necessitat de generalitzar i de manipular expressions algebraiques, ara investiguem noves generalitzacions de patrons visuals.
El primer patró l’he conduit jo, ara els toca a ells entomar-lo des de l’inici, i per això proporciono una guia que ajudi a ordenar les seves estratègies. Donat un patró visual, l’objectiu és trobar una expressió algebraica que a partir del pas (n) em doni el nombre d’objectes (quadrats, cubs, triangles, costats…).
Proposo un patró senzill i convido a seguir les preguntes de la Fawn Nguyen.
1. Com és el següent pas del patró? Dibuixa’l.
2. Fes un croquis del pas 43.
3. Completa la taula que relaciona el pas amb el nombre de quadrats.
4. Quina és l’expressió algebraica?
Aquestes preguntes guien el procés d’abstracció, i certament es de gran ajuda, però tinc la sensació que és convenient no forçar a seguir aquesta guia si no es vol, donat que cada alumnx té estratègies de resolució ben diferents.
Arribats aquí proposo alguns patrons concrets per tal d’incrementar la dificultat progressivament.
Com per exemple aquests dos per mostrar la relació entre el pas i el creiexement del patró, així com el creixement quadràtic.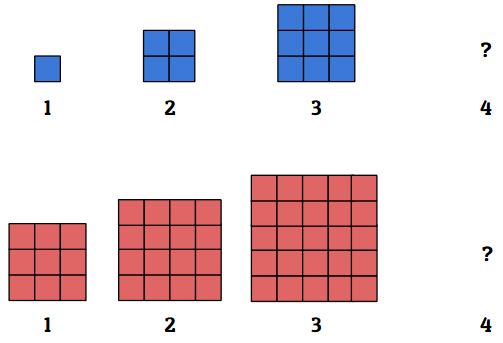
O aquest per introduir el creixement cúbic.
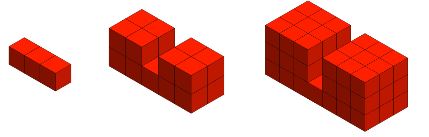 O aquest per fer sortir la suma dels n primer nombres, que no es resol d’una manera gaire intuïtiva, però que és una bellíssima interpretació visual de la demostració numèrica.
O aquest per fer sortir la suma dels n primer nombres, que no es resol d’una manera gaire intuïtiva, però que és una bellíssima interpretació visual de la demostració numèrica.
Arribats fins aquí explorem lliurement visualpatterns.org, individualment o per grups, com vulguin. De tant en tant demano si vol explicar-ne un a la pissarra.
Una metodologia que també em sol funcionar és donar a tothom el mateix full de patrons, com el de la imatge, posar-nos en grups i demanar que completin la taula de respostes a la pissarra a mesura que van descobrint expressions algebraiques, cosa que posa de manifest l’aprenentatge i ajuda a crear un clima de treball maco.
10/08/15. En Jordi Font m’envia un correu amb aquesta genial extensió:
Es pot fer una darrera part en la sessió proposada. Donar l’expressió algebraica i que siguin ells els que generen el patró: se n’adonen que hi ha diversos patrons amb una mateixa expressió algebraica. A partir d’aquí, es pot intentar cercar quines característiques geomètriques compateixen tots els models geomètrics mostrats a classe.
Crèdits: Abraham de la Fuente la idea primigènia. Fawn Nguyen la guia de l’alumnx i visualpatterns.org. Simon Greg el patró de ninots.
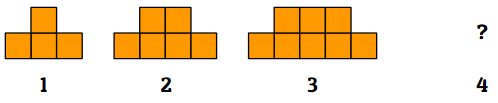

1 comentari